Видео начинаещи решение за графика на квадратно уравнение по предмета на алгебра в 8 клас

Уравнение на формата = 0, където ≠ 0 се нарича квадрат. Ако а = 0, тогава ще имаме линейно уравнение, и в този урок ние няма да ги разглеждаме.

Feature, където ≠ 0 се нарича квадратна функция. Графиката на тази функция е парабола. Ако> 0. клоновете на параболата са насочени нагоре. Ако, обаче,<0. то ветви параболы направлены вниз. Шаблоном для данной параболы является парабола .

=

= -

Единственият метод, който може да се реши с квадратно уравнение е сега - е графичен метод, който разгледаме следния пример.

За решаване на уравнението 0 =

Ние изграждане на графиката на функцията

Шаблон е графиката на

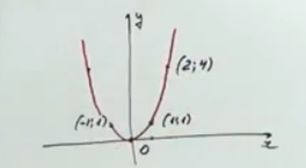
Фиг. 1. Илюстрация например

Така съградихме графиката на у = х 2. За да се построи графика на функцията, е необходимо да се движи в горната част на графиката. За да се разбере от къде да го преместите, има 2 начина:

1-ви начин. Изчислява се, и след това (с = 1; б = 2; С = -3)

= (-1) + 2 2 ∙ (-1) - 3 = -4

Тъй като вече знаем координатите на върха на параболата (1; 4), сега е върнат връх графика и получаване на желаното параболичен (което ще се пресичат оста х в точките (-3, 0) и (1, 0).

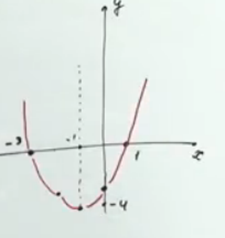
Фиг. 2. Илюстрация например втория метод

Корените на уравнението е точката на пресичане с оста х.

след това 2-ри Януари 2 ∙ 1 -3 = 0 0 = 0 (1 - корена на уравнението)

след това (-3) 2 + 2 ∙ (-3) - 3 = 0 0 = 0 (-3 - корена на уравнението)

Известно е, че всяка права линия (включително Ox) дисекция, в 2 х парабола точки. Тези точки ще представят, тогава проблемът е решен правилно.

Второ метод. Той трябва да се разпределят пълен квадрат.

За да се отчете 1, трябва да се движат на оригиналния парабола с 1 единица от ляво, и за отчитане на 4, което трябва да се измести параболата 4 единици надолу. И ние се графика на оригиналната функция. След това изпълнява актове, посочени в метод 1 m. Отговорът също няма.

Помислете за друг начин за решаване на една и съща формула:

функции на парцела и

Как да се изгради графика на функцията вече е известно, (това е модел парабола).

Графика на функцията конструира като се използва таблица:

След това направи графиките:

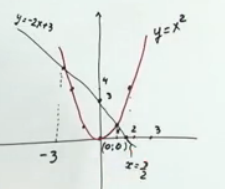
Фиг. 3. Илюстрация например

Чист чертеж показва, че графиките функционалните пресичат в точки с абсцисната 1 и -3. При проверка, ние потвърждаваме, че решението и са.

A: х = -3 и х = 1.

Предимството на този метод е, че ние сме изградили най-простият от всички възможни параболи. Въпреки това, ние също трябваше да се построи графика на линейна функция, но е лесно да се изгради. След това имам 2 точки на пресичане, идентифицирани абсциса, които трябва да бъдат проверени.

Разглеждане на уравнението в обща форма = 0, където

За да реши това уравнение, което трябва да:

1-ви път (парцел цялата функция)

а) Необходимо е да се конструира функция парабола с помощта на шаблон.

б) Да се ​​намери точката на пресичане с оста х, и ги закара до абсцисата.

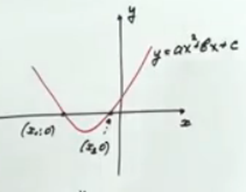
Фиг. 4. Илюстрация на пример В)

в) Прилагане взето от хоризонтален метод за превръщането им в уравнението и пиша отговор.

Метод 2 (секвестиращ член в)

а) изменение на уравнението поради поверителността :.

б) изграждане на парабола и една права линия.

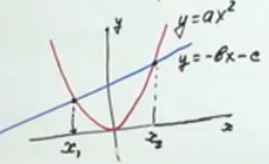
Фиг. Пример 5. Илюстрация б)

в) Намерете по абсцисата парцели точките на пресичане.

г) изпълнява взето от хоризонтален метод за превръщането им в уравнението и пиша отговор.

а), от уравнението може да бъде умножена по -1 termwise;

б) ръководи параболата не пресича повече от 2 точки.

От положителна гледна точка следва да се отбележи, че графичен метод може да разреши тези уравнения, ние не може да бъде решен аналитично.

Сред недостатъците разпределят това, което ние трябва да се чете, почти се познае по абсцисата (приблизителни методи - това минус).

Допълнителни препоръчани връзки към ресурси в Интернет

Ако откриете грешка или невалидна връзка, моля да ни уведомите - да даде своя принос за развитието на проекта.