Теорема и определяне геометрия (клас 2), истории
Първи втория урок, посветен проучване теореми аксиоми и определения 7 геометрия клас.
25. СОБСТВЕНОСТ перпендикулярна на линията - това е комплекс определение, което е 4 пъти думата "даде това", и никой от тях не е за изпускане. Четем от дадена точка, която се намира по дадена линия ТЕЗИ напред в тази полуравнина може да бъде само един ще повиши перпендикуляра.
26. ъглополовящата - полу-линията, която води началото си от горния ъгъл и пресича ъгъл.

- ако две страни и ъгъл. затворено между триъгълник са равни на две страни и ъгъла направи между тях, друга триъгълник, след триъгълници са равни;
- ако две съседни страна и към един ъгъл на триъгълника, съответно странична и съседен на него две други ъгли на триъгълника, тези триъгълници са равни;
- Ако трите страни на един триъгълник са равни на трите страни на друг триъгълник, то триъгълниците са равни.
Следствие. В равни триъгълници срещу равни страни са равни ъгли и срещу равни ъгли са равни страни.
28. Средна - сегмент, който свързва върха на триъгълника със средата на противоположната страна.
29. триъгълник ъглополовяща - сегмент ъглополовяща на ъгъла на триъгълника затворено между горната и на противоположната страна. В ъглополовяща има начало, но няма край, а в ъглополовяща на триъгълника е началото е краят.
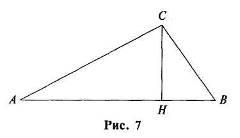
- височината на триъгълника - е перпендикулярен падна от върха на триъгълника, за да
противоположната страна или неговото продължаване;
- е перпендикуляра спада от върха на триъгълника на линията съдържащ противоположната страна.

- равнобедрен триъгълник - триъгълник, в който двете страни са равни.
Имоти - в равностранен триъгълник ъгли в основата са равни.
32. Имотът на равнобедрен триъгълник медианите:
- средната ъгъл при върха на равнобедрен триъгълник е и ъглополовящата и надморската височина.
33. Имуществото на двете прави, успоредни на трета:
- Ако две линии освен успоредни една и съща трета, а след това те са успоредни един на друг.

- в пресечната точка на двете прави линии, образувани от третата двойка едностранни четирите ъгъла, четири двойки са разположени напречни ъгли и 4 двойки съответните ъгли.
35. Признаците на паралелни линии:
- ако в пресечната точка на две прави трета Оказва се, че който и да е кръстосано лежи ъгли са равни, или каквито и съответните ъгли са равни, или всякаква едностранна добавите до 180 градуса, а след това тези линии са успоредни.
36. Имотът се лежи на кръст, съответно, и едностранно ъгли:
- Ако две успоредни линии се пресичат с една трета, напречно разположени ъгли са равни, съответните ъгли са равни и едностранни ъгли в размер, равен на 180 °.

Последици:
- в равностранен триъгълник, всички ъгли са равни на 60 °;
- в правоъгълен триъгълник е равна на сумата на острите ъгли на 90 °;
- правоъгълен равнобедрен триъгълник са остри ъгли на 45 °;
- в правоъгълен триъгълник крак лежи срещу ъгъл 30 ° на, равно на половината
хипотенуза;
- външен ъгъл на триъгълника е равна на сумата от двете вътрешни ъгли не са в близост до тях:
- Ако два ъгъла от един триъгълник са равни на два ъгъла от друг триъгълник, след това трети ъглите са те.

1. ако краката на триъгълника, съответно, равна на крака на друг триъгълник, то триъгълниците са равни;
2. ако съседен на него крак и остър ъгъл на триъгълника са равни съответно на крака и прилежаща към нея остър ъгъл на друг триъгълник, тези триъгълници са равни;
3. Ако катет срещу него и малък ъгъл на триъгълника са равни съответно на крака и срещу остър ъгъл към него друг триъгълник, тези триъгълници са равни;
4. ако хипотенуза и малък ъгъл на триъгълника и хипотенузата, съответно, равна на остър ъгъл от друга триъгълник, тези триъгълници са равни;
5. Ако хипотенузата и крака на един триъгълник са равни на хипотенузата и баща си на друг триъгълник, то триъгълниците са равни.
39. Теорема на уникалността на перпендикуляра спадна:
- от една точка извън линията на линията, можете да пуснете една перпендикулярна и само един.

- кръг - крива затворен в равнина, чиито точки са на еднакво разстояние от центъра на кръга;
- кръг - на равнината, ограничена от окръжност;
- акорд - отсечка, която свързва две точки от обиколката;
- диаметър - акорд, минаваща през центъра на кръга;
- радиус - сегмент свързване на централната точка на обиколката;
- дъга - част от обиколката;
- сектор - част от окръжност, затворена между два радиуса и дъга;
- сегмент - част от кръга, обвити между акорд и дъгата.
41. Мястото на точки (HMT) - всички точки на равнината или пространство,
които имат същите свойства.

пресече кръг.
43. вписан ъгъл и измерване му.
- включен ъгъл - ъгълът на върха на който се намира на кръг, и страните се пресичат кръга;
- вписан ъгъл се измерва от половината от дъга, на които се основава;
- включен ъгъл, равен на половината от центъра, от двете страни на които преминават през една и съща точка на обиколката и, че страната на периферен ъгъл, и ако вписан ъгъл е тъп, допълва половината централната до 180 °.

- три симетрия, перпендикулярна се пресичат в една точка, и тази точка е в центъра на кръга.
45. Второто триъгълник Център:
- трите ъглополовящи на ъгли на триъгълник се пресичат в една точка, а този момент
Той е в центъра на вписан кръг.
1 урок 3