Определяне на първата пространствена скорост за планетата, където масата и радиусът на двете

Състояние на проблема:

Определяне на първата космическа скорост за планетата, масата и радиуса на която е два пъти по-голяма от Земята.

№2.5.7 задача на "Сборник задачи, за да се подготвят за приемните изпити по физика UGNTU"

\ (R = 2R_3 \) \ (М = 2M_z \) \ (\ upsilon_1 - \)

Решение:

Първата космическа скорост - е процентът, който искате да кажете на тялото си, че тя се превръща в спътник на планетата. Тя може да се намери от следните съображения. Когато движението на сателит в кръгова орбита, на силата на гравитацията, тя се дава центростремителна ускорение, така че вторият закон на Нютон дава такова равенство:

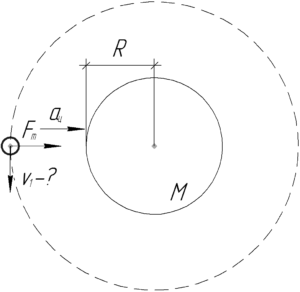
гравитационната сила може да се намери от закона за всемирното привличане, имайки предвид, че височината на орбитата е малък; тя е близо до Земята:

сателитна центростремителна ускорение, движещи се със скорост \ (\ upsilon_1 \), е равна на:

В уравнение (1) заменен израза (2) и (3):

Следователно първата пространствена скорост може да се определи по следната формула:

Чрез хипотеза \ (R = 2R_3 \) и \ (М = 2M_z \), поради:

По принцип, след получаване на тази формула може да се каже, че първата космическа скорост на тази планета е същата като тази на Земята. Но ние "ще постигне" задачата чрез.

Умножение и деление на фракции от корен на \ (R_3 \), тогава:

изразяване \ (>>>> \) е ускоряването на свободно падане \ (ж \) в близост до земната повърхност, в резултат на това ние имаме:

Спомнете си, че радиусът на Земята е 6.4 · 10 6 m, така че цифровата Отговорът е:

A: 8000 м / сек.

Ако ви харесва на проблема и неговото решение, можете да го споделите с приятелите си, като с помощта на тези бутони.