Идентифициране и намиране границите
тестване онлайн
Границата на определяне последователност
номер се нарича границата на числова последователност, ако има произволен брой, така че за всички п> N неравенството
Когато броят ограничение номер на последователност (хп). след това да напишете:
ПРИМЕР 1 разгледаме номериране. Ние намираме първите няколко елементи на тази последователност:
Елементи на числова последователност ще показват точките в координатна ос:
Лесно е да се забележи, че елементите, които представляват елементи на последователността на номериране с увеличаването на п номера идват все по-близо до точката, приближаващ = 1. Разстоянието от точка А до Xn = 1, може да бъде по-малко или всяко положително число.
Когато поредицата има лимит, той се нарича приближаващите се. Когато границата на последователност е номер. кажем, че последователността (хп) клони към.
(В нашия пример, последователността клони към 1).
Когато поредицата е без лимит, той се нарича разходящ.
От дефиницията на граничната последователност че
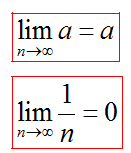
Аритметични операции на сходни секвенции

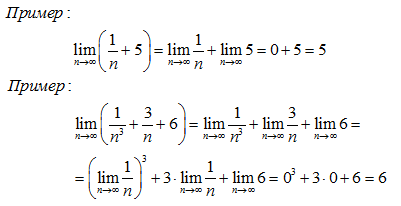
Определянето на лимит функция
Редица нарича граница на функция у = F (X) в точка x0. ако за всяко положително цяло число съществува положително число такова, че за всички х. които удовлетворяват неравенството:
Когато номер е границата на F функция (х). след това да напишете:
Обърнете внимание! Тук х клони към определен брой, но не до безкрайност. Аритметични операции за определени функции, подобни на тези граници.
Методи за решаване граници
При подреждането на ограничението на съотношението на два полиноми в х, ако двете членове на връзката е полезно да се разделят х п. където п - най-висока степен на полиноми.
Видовете граници решения, където р (х) и Q (х) - цяло число полиноми. Ако P (x0) = Q (x0) = 0. е препоръчително да се намали фракция.
Изразяване съдържащи ирационалност. дава на рационалния ум, в много случаи, чрез въвеждане на нова променлива.
Друг начин за справяне с ограниченията за ирационални изрази - превод на ирационалността на числителя на знаменателя, или, обратно, от знаменателя в числителя.
При изчисляване на сроковете, в много случаи, формулата се използва
Намирането на границите на формата
При решаването на тези граници често използват формула на напр.
Някои важни ограничения:
