Място теорема
теорема I. на Wyeth за над квадратното уравнение.
Сума понижено корените на квадратното уравнение х 2 + пиксела + р = 0 е равна на втората коефициент, взет с обратен знак, и продукта от корените е равна на постоянен Терминът:
Намерете корените на над квадратно уравнение с помощта на теоремата Vieta му.
Пример 1) х 2 -X-30 = 0. Това доведе квадратно уравнение (х 2 + пиксела + р = 0). втори коефициент р = 1. и константа Q = -30. Първо се уверете, че уравнението има корени, а корените (ако има такива), ще бъдат изразени в цели числа. Това е достатъчно, че дискриминантата е точен квадрат число.
Намираме дискриминантен D = б 2 - 4ав = (- 1) 1 2 -4 ∙ ∙ (-30) = 1 + 120 = 121 = 11 2.
Сега, от Теорема Vieta сума от корените трябва да е равна на втората коефициент, взето с обратен знак, т.е. (-p), и продуктът е равна на постоянен план, т.е. (Q). След това:
Пример 2) х 2 + 6x + 8 = 0. Ние дадохме квадратно уравнение с втори коефициент р = 6 и Q = свободно елемент 8. Уверете се, че там са цели числа корени. Намираме дискриминантен D1. като втори коефициент - четен брой. D1 = -1 ∙ 2 март 8 = 9-8 = 1 = 1 2. дискриминантен D1 е идеален квадрат номер 1. означава корени на уравнението са цели числа. Ние вземете корените на теоремата Място: сумата на корените е р = -6. и продукт на корените е равно на р = 8. Този номер -2 и -4.
Пример 3) х 2 + 2х-4 = 0. Това намалява квадратно уравнение втори коефициент р = 2. и константа Q = -4. Намираме дискриминантен D1. като втори коефициент - четен брой. D1 = 01 февруари -1 ∙ (-4) = 1 + 4 = 5. В дискриминантата не е точен квадрат брой, така че можем да заключим. корените на това уравнение не са цели числа и да ги намерят невъзможно Vieta теорема. Следователно, ние решаване на това уравнение, както обикновено, чрез формулите (в този случай, формулите за конкретния случай на дори Вторият фактор). получаваме:
Пример 4). Направи квадратно уравнение за своите корени, ако x1 = -7, Х2 = 4.
Пример 5). Направете квадратно уравнение за своите корени, ако:
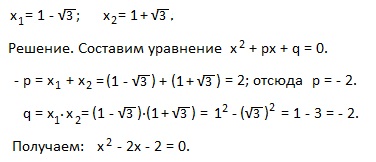
II. теорема Wyeth за пълно квадратно уравнение брадва 2 + BX + С = 0.
корени сума е равна на минус б. разделени от. продукт на корените е равна. разделени от:
Пример 6). Виж сумата от квадратни корени на уравнението 2x 2 -7x-11 = 0.
Виждаме, че това уравнение ще има корени. Това е достатъчно, за да израз за дискриминантата и без това изчисление, само за да се уверите, че дискриминантата е по-голяма от нула. D = 07 Февруари -4 ∙ 2 ∙ (-11)> 0. Сега ние използваме teoremoyVieta за пълни квадратно уравнение.
Пример 7). Виж продукта от корените на квадратно уравнение 3x 2 + 8x-21 = 0.