Какъв е срокът за това как да го намеря
Общата концепция за ограничение: има ограничение броя на определена променлива, ако в процеса на промяна на стойността на тази променлива е безкрайно близо до.
Нека обясним това с един пример, който показва също. След пример нека общите граници разтвор алгоритъм.
В допълнение, решен в този урок примери и всякакви други задачи, от външната страна, можете да проверите на границите на онлайн калкулатор.
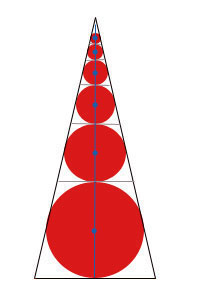
В долната част на равнобедрен триъгълник вписан кръг. Диаметърът на кръга обозначен с. Фигура диаметър conected синьо. До кръг, успоредна на основата на допирателните на оригиналната триъгълник (е фигурата на сиво). Резултатът е триъгълник, подобен на оригинала. В този триъгълник е точно вписан кръг. Диаметърът му - (диаметър на фигурата, обградени допирателни). Подобни конструкции са в ход, като се допуска височината на триъгълника. Получените последователно по-малки кръгове и съответната последователност на дължините на техните диаметри. Тази последователност дължини диаметри дава пример за променлива, която се увеличава с неограничен брой обиколка х клони към нула. Границата на тази последователност е нула :.
Нека пишат дадения пример на езика формула. Така че, броят на кръг увеличава и клони към безкрайност, разбира се. Да предположим, че е равнобедрен триъгълник, че дължината на диаметъра на всеки кръг вписан в него се изчислява съгласно формулата
Стойността, че трябва да се намери, ще бъде записано, както следва:
Лим това е границата, и посочи, променлива под него, който се стреми към определена стойност - нула, всеки друг номер, безкрайност.
Сега ние се изчисли граница чрез задаване на променливата х е безкрайна (в тесния определение се нарича "завърши на определението за функция", с това определение, можете да видите на глава "Лимит" в следните части). Да приемем, че краен количество, разделено на безкрайност е нула:
Тъй като се счита последователност от кръговете свързват други променливи - последователността им диаметри сума:
След като разгледа снимката отново, ние откриваме, че лимитът на последователността е равна ч - височина на равнобедрен триъгълник. Като цяло, ограничение може да е нула, всеки друг номер или безкрайност.
Сега, по-строгото определение на границата на функция, която можете да зададете на изпита, както и за разбирането на които ще изисква малко повече внимание.
Да предположим, че F функция (X), определена на набор, и нека X е точка. Извадете свързва точки X, различни от:
приближава до. Стойностите на функцията на точки на последователност също образуват цифрова последователност
и е възможно да се повдигне въпроса за съществуването на своя лимит.
ОПРЕДЕЛЕНИЕ 1. брой нарича граница на F функция (х) на мястото (или), ако за всяка последователност клони към (1) стойностите на аргумент х. от съответната последователност (2) клони към А.
Символично, то се изписва така:
Това означава: да намерите границата на функцията, е необходимо да се функцията за х заместител на търсената от х стойност.
Пример 1. Намерете границата на функцията на.
Решение. Заместител х стойност вместо 0. получаване на:
По този начин, срокът на функцията, когато е едно.
В допълнение, решен в този урок примери и всякакви други задачи, от външната страна, е възможно да се провери на границите на онлайн калкулатор.
Граница на функция на това кога и
В допълнение към преценката на понятието граница на функция, когато там е и концепцията за граница на функцията, когато аргументът клони към безкрайност.
2. Определяне на броя А се нарича граница на F функция (х) когато, ако за всяка безкрайна последователност от (1) на съответната последователност на аргумент стойности (2) на функцията клони към А.
Символично е писано като.
Определение 3. брой нарича граница на F функция (х) при (), ако по някаква безкрайна последователност на аргумент стойности, елементи, които са положителни (отрицателен) последователност, съответстваща на (2) стойностите на функцията клони към А.
Символично това се изписва така: ().
Това, както в случая с Определение 1, означава: да намерите граница функция, трябва да се работи за х заместител безкрайност плюс безкрайност или минус безкрайност.
Пример 2. Намерете границата на функцията на.
Решение. Заместител на х безкрайност. Тази последователност на функцията е безкрайно, и следователно има горна граница е равна на нула:
За по-голяма яснота и надеждност при вземането на решение за пример в проекта, можете да заместите за х броя на superlarge. Можете да получите supersmall номер, когато разделя.
И провери на решение за границите на възможни ограничения на калкулатора онлайн.
Теорема 1. (функция в рамките на една). Функцията не може да има повече от една точка.
Следствие. Ако F две функции (х) и г (х) са в съседство на точка, с изключение може би най-точка, или те са еднакви на границата, или и двете не са ограничение в този момент.
Теорема 2. Ако F функция (х) и г (х) има ограничения в точката, тогава:
1) ограничи алгебрични сумата от функции е равна на сумата от алгебрични условия граници, т.е.
2) граница на функцията продукт е продукт на границите на фактори. т.е.
3) границата на отношението на две функции е равно на отношението на срока на дивидента от границата на делител ако граница делител не е нула, т.е.
Забележка. Формула (3) и (4) притежават за всеки определен брой функции.
Следствие 1.Predel постоянно е много постоянен. т.е.
2.Postoyanny Коефициентът на разследване може да се приема като знак на срока. т.е.
Пример лимит 3. Find:
И провери на решение за границите на възможни ограничения на калкулатора онлайн.
Пример 4 лимит търсене:
Решение. Уверете се, че граничната делител не е равна на нула:
По този начин, с формула (5) се прилага, и следователно,
И провери на решение за границите на възможни ограничения на калкулатора онлайн.
Теорема 3 (на границата на съставна функция). Ако има краен срок
и F на функция (и) е непрекъсната в точка, тогава
С други думи, на границата на непрекъснатост символи и функции могат да бъдат разменени.
Директен прилагане на теоремите за граници, обаче, не винаги водят до целта. Например, не е възможно да се приложи теоремата на границата на частния, ако срокът на делителя е нула. В такива случаи, трябва първо да конвертирате еднакво действие, за да може да се прилага следствие от Теорема 1.
Пример граница 5. търсене:
Решение. Теоремата на границата на частния тук не важи, тъй като
Трансформирайте дадена фракция чрез разширяване на числителя и знаменателя от факторите. В числителя получаваме
корените на квадратното трином (ако сте забравили как да се реши квадратно уравнение, отидете тук). Сега ние нарязани фракция и от следствие от Теорема 1, се изчислява границата на функцията:
Проверете разтвора до границите на възможни ограничения на калкулатора онлайн.
В решението на пример 5, ние вече са се срещали невзрачен. Тази несигурност и несигурността на формата - най-често несигурността, която се изисква да разкриват при решаването граници.
Много от проблемите, от външната страна, получава студентите, просто носят такава несигурност. За тяхното разкриване или по-точно, като се избягва несигурността, има няколко метода за изкуствен трансформация на формата на изразяване по граничната знак. Тези методи са както следва: Терминът разделяне на числителя и знаменателя от висш ниво на променливата, размножаването чрез експресия на конюгат и факторинг за последващото намаляване, като се използват разтвори на квадратно уравнение и формули на съкратената умножение.
Овладейте тези техники с примери.
За да се преобразуват изрази изискват ръчни действия с правомощия и корени, както и операции с фракции.
Пример 6. Разширете несигурност и да се намери границата.
Решение. Ето, най-високата мощност на индексът п е равно на 2. Ето защо, терминът по план, ние разделяме числителя и знаменателя:
Ние получи отговори на този лимит функция на една променлива тенденция към безкрайност равни.
Проверете разтвора до границите на възможни ограничения на калкулатора онлайн.
Пример 7. Разширяване на несигурност и да се намери границата.
Решение. Ето, най-високата мощност на променлив х е равно на 1. Следователно, терминът по план, ние разделяме числителя и знаменателя от х:
Получи отговор на този лимит функция на една променлива тенденция към безкрайност е нула.
Проверете разтвора до границите на възможни ограничения на калкулатора онлайн.
Пример 8. Разширяване несигурност и да се намери границата.
Решение. В числителя - разликата между кубчетата. Ние го разшири до множители, като се използва формулата на съкратена процент умножение на училище математика:
Ние пишете израза, в резултат на трансформацията и да намери границата на:
Проверете разтвора до границите на възможни ограничения на калкулатора онлайн.
Пример 9. Разширяване несигурност и да се намери на границата на
Решение. Теоремата на границата на частния тук не важи, тъй като
Следователно, идентичността трансформира фракция: умножаване на числителя и знаменателя от биномно конюгат знаменател, и намалява с х 1. Според следствие от Теорема 1, получаваме израз решат кой намерите желания лимит:
Проверете разтвора до границите на възможни ограничения на калкулатора онлайн.
Пример 10. Разширяване на несигурност и да се намери на границата на
Решение. Директен заместване на стойността х = 0 в предварително определена функция води до несигурност на формата 0/0. За да се разкрие, изпълняват еднакви трансформации ще свърши с желаната граница:
Проверете разтвора до границите на възможни ограничения на калкулатора онлайн.