WolframAlpha на Руски троен интеграл в волфрам, алфа

За да намерите троен интеграл Wolfram | Alpha, използвайте следния синтаксис (а не се интегрират допуска съкратена версия вътр):

• интегрират ЮЯ dxdydz

Моля, имайте предвид, че тук, както и за двойни интеграли. за Wolfram | Alpha е много важно от порядъка на диференциалите DX запис, Dy и DZ в vyrazhnenii на подинтегрален, което определя последователността на ре-интеграция.

Като цяло, в резултат, който показва Wolfram | Alpha, зависи от последователността, в която се извършва реинтеграцията (реда, в който писмено DX, ди и DZ). Сравнете, например, предишния пример с следното:

• интегрират ЮЯ dydzdx

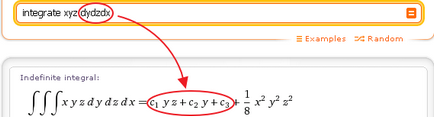
За да се изчисли определена троен интеграл. трябва правилно посочва границите на интеграция.

Ако всички граници на константи интеграция. Записът на заповед DX, ди и DZ няма значение. Например,

• интегрира х ^ 2y + YZ ^ 3 + 1 dxdydz, х = 0..1, у = -1..1, Z = -1..0

Същото важи, когато става въпрос за изчисляване на тройни интеграли с безкрайни граници:

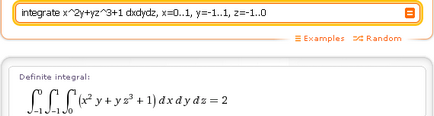
• интегрира 1 / корен (PI) д ^ (- (х ^ 2 + Y ^ 2 + Z ^ 2)) dxdydz, х = -oo..oo, у = -oo..oo, Z = -oo..oo

Въпреки това, ако се има предвид в тройни неразделна променливи граници на интеграция. Записът на заповед DX, ди и DZ отново става важно. Не трябва да забравяме, че DX, Dy и Dz при изчисляването на троен интеграл в Wolfram | Alpha непременно трябва да напишете в обратен ред на реда, които трябва да бъдат повторно интегриране в изчисляването на троен интеграл. А именно, както е показано в този пример:

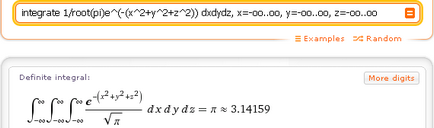
• интегрира XY ^ 2 + YZ ^ 2 + ZX ^ 2 dzdydx, Z = xy..root (х ^ 2 + 2у ^ 2), у = х ^ 2..root (х), х = 0..1

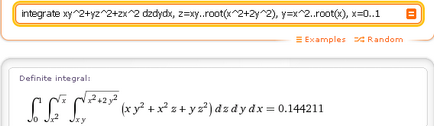
Както можете да видите, тук реда на изчисление на троен интеграл, както следва: на първо място "отнема" вътрешния интеграл от DZ (границите на интеграция, в която зависят от х и у), след това - с ди (лимити за интеграция на променливата у зависи от х), и най-накрая " взето "извън интеграл DX. Ето защо в края на подинтегрален е израз dzdydx (последователността е важно!).