Теорема Wyeth, с примери на формула

Един метод за използване на квадратното уравнение е формула Wyeth. който е кръстен Fransua Vieta.

Той е известен адвокат, и служи в 16-ти век френският крал. В свободното си време той ангажирани в областта на астрономията и математиката. Той установява връзка между корените и коефициентите на квадратно уравнение.

1. прилагане на формулата, можете бързо да се намери решение. Тъй като не е необходимо да въведете второто коефициент на квадрат, а след това се изважда от него 4ав, намирането дискриминантен заместител на стойността във формулата за намиране на корените.

2. Не може да се определи решението корените на знаците, вземете корените на проблема.

3. Решаване на система от два записа, че е лесно да се намери самите корени. В горното уравнение квадратен сумата на корените е равна на стойността на втория коефициент със знак минус. Произведение квадратен корен в горното уравнение е равна на третия фактор.

4. Според корените на квадратно уравнение да пишат, това е, за решаване на обратната задача. Например, този метод се използва за решаване на проблеми в теоретична механика.

5. Той е удобен за прилагане на формулата, когато водещият коефициент е равен на едно.

Място теорема 8 клас

формула
Ако X1 и Х2 - корените на горе квадратно уравнение х 2 + пиксела + р = 0. е:

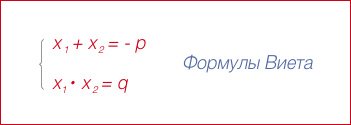
примери
X1 = 1; Х2 = 3 - корени х 2 - 2х - 3 = 0.

антоним

формула
Ако номера x1 на. x2. Р, Q, свързан с термините:

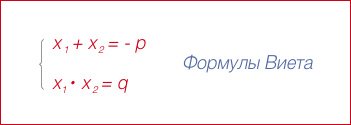
на X1 и X2 - корените на уравнение х 2 + PX + р = 0.

пример
Ние образуват квадратно уравнение за корените:

Вие уравнение има формата: х 2 - 4x + 1 = 0.

Място теорема за квадратно уравнение.

правило
Ако X1 и Х2 - брадва квадратни корени на уравнението 2 + BX + C = 0 тогава

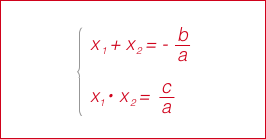
пример
X1 = 1,5 и Х2 = 2 - корените на квадратното уравнение 2x 2 - 7х + 6.