Свойства на функцията разбор на примера
За да се разбере тази тема, помислете за функцията. // показано в диаграмата показва как да функционира графика за определяне на неговите свойства.
Разбор функционални свойства на примера
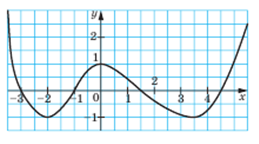
Yavl домейн на функцията. интервал [3,5; 5,5].
Диапазонът на стойностите yavl функция. интервал [1; 3].
1. Когато х = -3, х = - 1, х = 1,5, х = 4,5 стойността на функцията е нула.
стойност на аргумента, при която стойността на функция е нула, нула, наречена функция.
//t.e. За тази функция номера -3, -1, 1.5; 4.5 са нули.
2. На интервали от [4,5; 3) и (1; 1,5) и (4,5; 5,5] графика е се намира над хоризонталната ос, и на интервали от (-3, -1) и (1,5; 4,5) под оста абсциса, е обяснено така на интервали [4,5; 3) и (1; 1,5) и (4,5; 5,5] функция се положителна стойност, и интервалите (-3, -1) и ( 1,5; 4,5) са отрицателни.
Всеки един от тези периоди (когато функцията приема стойността на един и същ знак) се определя като разлика от постоянно Сигнум f.//t.e. например, ако вземем интервала (0, 3), тогава не е разлика от постоянен знак на функцията.
В математиката, приема през интервали от постоянна функция за търсене знак да се посочат максимални интервали дължина. //T.e. време (2, 3) е период на постоянно знак функция е, но трябва да бъдат включени в интервала на отговор [4,5; 3) съдържа процеп (2, 3).
3. Ако подвижната абсцисната ос от 4.5 до 2, може да се види, че графиката на функция върви надолу, т.е. стойностите на функцията намалява. // В математика кажем, че на интервала [4,5; 2] функция намалява.
С увеличаване х от 0 до 2 функция графика върви нагоре, т.е. функционални стойности се увеличават. // В математика кажем, че на интервала [2; 0] функция увеличава.
F Функцията се увеличава на интервал. Ако такава, че х2> x1, отговаря F неравенството е (х2)> (х1) за всеки две стойности X1 и X2 на аргумента на този интервал. // извикване на функция или увеличаване на интервал. Ако по някаква аргумент стойности на този интервал по-голямата стойност на аргумента съответства на по-голяма стойност на функцията .// т.е.. колкото по-голям Х, толкова по-добре.
F Функцията намалява на някои интервал. ако за всеки две стойности X1 и X2 на аргумента на този интервал, така че х2> x1, отговаря на неравенство F (х2) намаляване на някои интервал, ако за всички аргументи стойности на този интервал по-голямата стойност на аргумента съответства на минимална стойност на функцията. //t.e. по-голяма от х, толкова по-малко.
Ако функцията се увеличава в цялата област на определение, а след това той се нарича увеличава.
Ако функцията намалява в цялата област, а след това той се нарича намаляване.
Пример 1. графика съответно увеличаване и намаляване функции.
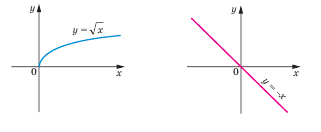
Определя yavl. дали линейна функция F (х) = 3x + 5 увеличаване или намаляване?
Доказателство. определения Vosprolzuemsya. Нека x1 и x2 са произволни стойности на аргумента, а x1 Получава се от заместване F (х1) е (х2) = (x1 + 3 * 5) (3 * х2 + 5) = 3 * x1 + 3 5 5 * Х2- = 3 * х2 = h1-3 * 1-3 * 3 * 7 = 3-21 = -19<0 Ние считаме, че е (x1) е (х2) <0,а значит f (x1) Имам нужда от помощ в училище?