определение на производно

В тази статия ще дам основни понятия, които ще се основават всички по-нататъшни теория на производната на функция на една променлива.

Път X - F на аргумент функция (х), и - малък брой не е нула.

(Прочетена "Делта X") се нарича нарастването на аргумента. На фигурата червената линия показва промяната в аргумента на стойността на х към стойността (тук се вижда, са имената на "увеличение" аргумент).

Когато се преминава от стойността на аргумента на стойността на функцията съответно да варира от подлежи на монотонност на сегмента. Разликата се нарича увеличение функция е една (X). съответстващ на това нарастване на аргумента. Фигурата показва увеличение функция синята линия.

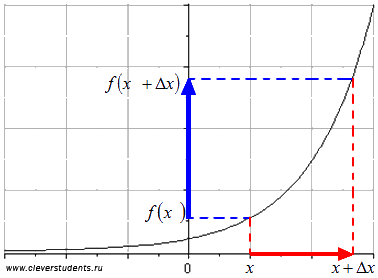
Помислете за тези понятия в конкретен пример.

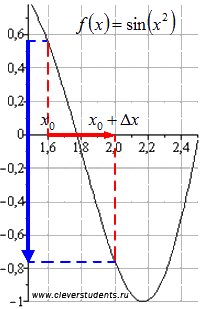
Вземете, например, функция. Fix точка и нарастването на аргумента. В този случай, нарастването на функцията в прехода от все още да е

Намалява каза на функцията на разпад на интервала.

Определяне на производно на функция в точка.

Да предположим, че F функция (X), определена на интервала (а, Ь). и - на мястото на този период. Производно с F функция (X) в точка, наречена граница на съотношението на добавката към функция аргумент нарастване с. Посочено.

Кога е последният срок, не предприеме конкретни крайна величина, а след това се говори за съществуването на краен производна в точка. Ако ограничението е безкрайна, а след това ние казваме, че производната е безкрайна в този момент. Ако срокът не съществува, а след това на производната на функцията на този етап не съществува.

е (х) функция се нарича диференцируема в точката, когато има ограничен производно него.

Ако F функция (х) е диференцируема във всяка точка на интервала (а, Ь). функцията се нарича диференцируема в този интервал. По този начин, всяка точка х в интервала (а, б) може да бъде свързана със стойността на функцията производно в този момент, това е, ние сме в състояние да определи нова функция, която се нарича производното на F функция (х) на интервала (а, Ь).

Операцията за намиране на производното се нарича диференциация.

Равен разлика в характера на понятията за функцията производно в точка и на интервал: производното на функцията на мястото - това е броят и производната на функцията в интервала - това е функция.

Намерете производната на функция в точка, като се използва определението.

Тъй като ние търсим производна на функцията в интервала, тогава отговорът трябва да се включи функция. Вземете, където х - всяко число от интервала. По дефиниция, производното е граница на съотношението на функцията на нарастване на нарастване на аргумента, за нарастване на аргумента клони към нула:

Така стигнахме до тази несигурност. За тези граници, използвайки размножаването чрез експресия на конюгат, последвано от прилагането на формули Acronym умножаване задействане на тези термини и съкращения:

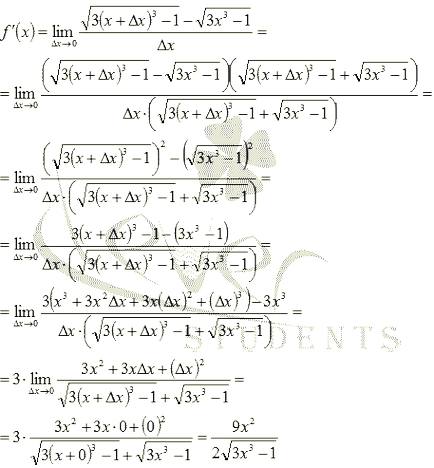
Нека да се съсредоточи върху един много важен момент: областта на F на функция (х) не винаги съвпада с домейна на деривата. Отбележете, че в предишния пример, областта на функцията е първоначалната интервал, и производното определя в интервала. Това, което искам да кажа. Така че, когато диференциране идеално отговорът е: функцията е производно на F функция (X) в интервала

Въз основа на дефиницията на производно с формула получава много маси, получени основните елементарни функции, които значително ускоряване на диференциацията. Концепцията на деривата се използва също и в доказателство на правилата за получаване на производни.