Начин на нередовно движение
Сега ще разгледаме нередовно движение - това е движението в които абсолютната стойност на промените в проценти с течение на времето. Оказва се, че там е проста геометрична интерпретация на пътя, изминат от тялото на произволно движение.
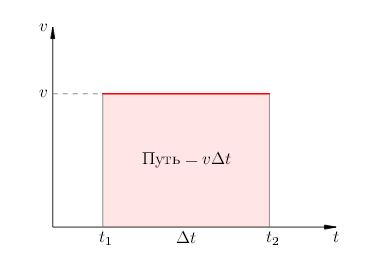
Нека започнем с еднакъв движение. Нека скоростта на тялото е постоянна и равна. Нека вземем две точки във времето: отправна точка и крайна точка. Продължителността на определен интервал от време, равен.
Очевидно е, че за периода от време, тялото преминава през пътя:
Да изградим графика на скоростта в зависимост от времето. В този случай ще бъде права линия, успоредна на оста х (фиг. 1).
Фиг. 1. Път в униформа движение
Лесно е да се види, че изминатото разстояние се равнява на площта на правоъгълник, разположена под скоростта на хартията. В действителност, първият фактор в уравнение (1) има вертикална страна на правоъгълника и Вторият фактор - нейната хоризонтална страна.
Сега ние трябва да се обобщи геометричната интерпретация в случай на нееднакво движение.
Нека скоростта на тялото зависи от времето и на разглеждания интервал скорост графиката изглежда по следния начин (фигура 2):
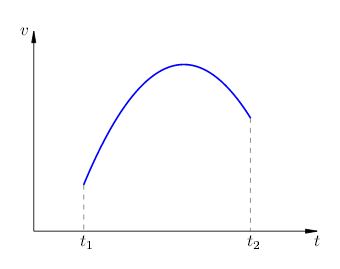
Фиг. 2. Неравномерното движение
Тогава ние се спори, както следва.
1. Ние разделяме нашето период от време в малка стойност сегменти.
2. Да приемем, че във всеки такъв сегмент тяло се движи с постоянна скорост. Това означава, че плавна промяна на скоростта на мястото на скорост приближение *: за всеки малък интервал от време тялото се движи равномерно, а след това скоростта на тялото веднага и промени ckachkom.
Фиг. 3 показва две пристъпи приближение. Ширината на стъпалата на десния фигурата по-малко от половината от ляво.
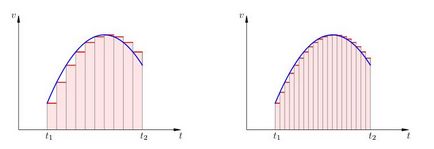
Фиг. 3. Активизира приближение
Пътят пресича по време на движение униформа - района на правоъгълник се намира под стъпка. Затова пътят пресича за всички времена такава "отстъпи" движение - е сумата от площите на всички правоъгълници върху графиката.
3. Сега клони към нула. Ясно е, че скоростта ни ще се включи приближение към първоначалното ограничение на скоростта на графиката на фиг. 2. Сумата от областта на правоъгълници ще влязат в зоната под графиката на скоростта; Ето защо, тази област е пътят пресича от тялото за известно време преди това. (Фиг. 4
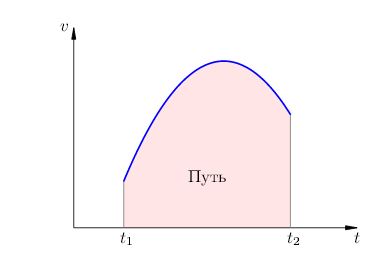
Фиг. 4. Начинът, по неравномерно движение
В резултат на това ние се стигне до нас желания да се правят обобщения геометричната интерпретация на пътя, по-горе, получена за случай на единна движение.
Сближаване - е приблизителният замяната на един доста сложен обект прост модел, който е по-удобен за изследване.
Геометричната интерпретация на пътя. Пътят пресича от тялото на всяко движение, равна на площта под графиката на скоростта на предварително определено време интервал.
Нека да видим как тази геометрична интерпретация на важен специален случай на равномерно ускорено движение.
Задача. Орган, имащ скорост в началния момент. Той ускорява с постоянно ускорение. Намери пътя пресича от тялото до точка във времето.
Решение. Времевата зависимост от скоростта в този случай има следния вид:
график скорост - прави, е показана на фиг. 5. Да се стремиш към начина, по който има трапец площ, разположена под скоростта на хартията.
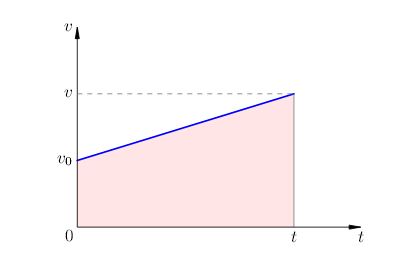
Фиг. 5. пътя с равномерно ускорено движение
По-малката основа на трапеца са равни. Големи основания пука. Височината на трапеца е равен. Тъй като площта на трапец е продукт на половината сума от бази на високо, трябва:
Тази формула може да бъде пренаписана в по-запознати форма:
Тя, разбира се, добре известен на вас от темата "Равномерно ускорено движение."
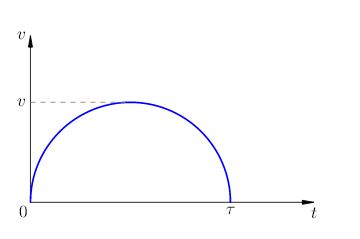
Задача. скорост Графика тяло е полукръг диаметър (фиг. 6). Максималната скорост на тялото е равна. Намери пътя пресича от организма с течение на времето.
Решение. Както знаете, площта на кръг с радиус равен. Но този проблем трябва да се вземе предвид, че радиусите на полукръговете имат различни измерения: хоризонталната радиуса е време. и по вертикала е скоростта.
Ето защо, изминатото разстояние, което се изчислява като площта на полукръга се равнява на половината от продукта на хоризонтална и вертикална радиус радиус: