Как да се намери обемът на куб версия на проблема и тяхното решение

Как да намерите елементите на куба на своя страна?

Тъй като линия оформя - квадратна, площта му се определя от формулата №1, в който известно количество, необходимо за квадратен:

Диагонал от всяка страна се изчислява по формула №2, която страна е умножена по корена на 2:

Предишна формула получен от Питагоровата теорема. Лесно е да се разбере, ако видите, че диагонални аспекти - е хипотенузата на правоъгълен триъгълник. И краката на неговата страна на площада са.

За да определите дължината на диагонала на куба, ще трябва по следната формула №3, съдържащ определен начин и корен квадратен от 3:

Тя също се извлича от питагорова теорема. Точно както хипотенузата служи желаното диагонал. Краката са една и съща страна на площада и диагонала.

Понякога е необходимо да се знае формулата за изчисляване на площта на страничната повърхност на фигурата. Той е умножено по квадрата на страна 4. Тук е (№4):

Разберете как да се получи тази формула, че е лесно. Страната е изправена - 4. Това означава, че общата им площ - четворна стойността на площта на един квадрат.

Ако искате да се определи площта на цялата повърхност. след това се използва този запис в която ushesteryaetsya квадратен ребро (Формула №5):

Той се получава подобна на предходната формула, само броя на квадрати се увеличи до 6.

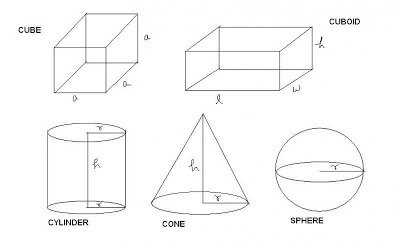
Каква е силата на звука?

Казано просто, това е място, което заема всеки орган в пространството. Всеки субект е ограничено в пространството повърхности. Може да има няколко, но има случаи, в които само един. Например, ако в тялото - това е една топка. Но тези повърхности са непременно затворени. Пространството, която заема геометричната тялото, и ще бъде си капацитет, или обем.

обем единици

Когато става въпрос за твърди частици, количеството единици винаги ще бъде кубически размер. Например, метър, сантиметър или километър кубчета. За течности, взети литра, които са изразени чрез кубичен дециметър. Но ако те заемат много големи количества, те също се измерва в кубични метри. Например, ако водното количество, регистрирано в апартамента се счита в м 3. Както се оказва, че е по-удобно и по-лесно да числено.

Метод 1: Разберете обема на куб, ако е известен страничен

Това е най-простият метод, който ще ви кажа как да се намери обемът на куб. Той е просто да се изгради на стойността на тази част от трета степен. С други думи, трябва да се умножи на страната три пъти. По аналогия с произволна форма на паралелепипед, когато е необходимо да се размножават всички линейни измерения. Формулата се изписва като (№6):

Метод 2: цялата повърхност на познат

В този случай е необходимо да се разделят на известна стойност за корен квадратен 6. От междинно съединение отговор и изгради редица кубически метра. Ако пишем тази формула, ще получите следното (№7):

Метод 3: куб лице диагонал е дадено

С цел да се знае как да се изчисли обема на куб, в който случай трябва да извършите следните стъпки. Първо, изграждане на някои значение в куба, и след това се умножава по корен квадратен от 2 и разделете на 4. Формулата на този проблем (№8):

Това уравнение се получава както следва: определен размер трябва да бъде разделена на квадратния корен на две. Тогава броят доведена до трета степен. След извършване на преобразуване, получен в числителя на куба диагонал и знаменателят 2√2. Математика изисква функция не е ирационално. Затова се разпорежда с него, като се умножи по √2. Тогава се появява числителя √2, а знаменателят се получава 4.

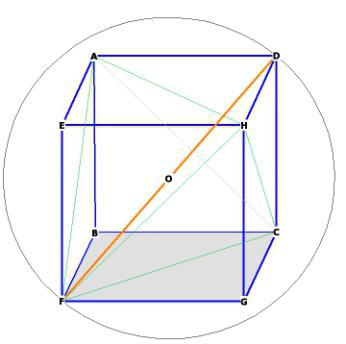
Метод 4: Диагонален куб

Формула, която ще ви кажа как да се намери обемът на куб ще съдържа стъпки: квадратура диагонала, умножена по корен квадратен от 3, и разделението на само 9. Той ще бъде записано като (№9):

Подобно на предходните претенции, в първите диагонални записи, разделен на корен квадратен от три и се повишава до куба. След промените в знаменателя също изглежда ирационален, от която искате да отидете. Така че, има стойност в √3 на числителя и под линията - 9.

примери на задачи

първата задача. Дан куб с ръб 12 см. Изчислете обема си и да изразят отговора в квадратни метри.

В тази задача, той ще бъде по-трудно да се преведат на отговор в други звена, вие решавате как да се намери обемът на куб. За извършване на първата част от задачата: Формула записан под номер 6. След куба 12 ще отговори номер 1728 cm 3. Сега ние трябва да помним, как да ги преведат в кубически метра. За тази цел, отговорът трябва да бъде разделена на 100 три пъти. Сто идва от факта, че един метър е сто сантиметра. Разделянето се извършва три пъти, тъй като единица куб в работата. Така че, в 1728, разделен на 100 ще даде 17.28. След втора дивизия ще 0.1728. Третият акт ще отговори 0.001728 m 3. Това е отговорът на проблема: обемът на куб е равно на 0.001728 m 3.

Втората цел. Има един куб с площ от цялата повърхност на 600 DM 2. Намерете обема на данните и да го изразя в кубични метри.

За да се отговори на въпроса на тази задача ще се нуждаят от формула номер 7. Първото действие на определен брой се дели на 6. Отговорът превръща 100. От това, че е лесно да се вземе корен квадратен, той ще бъде равен на 10. Сега трябва да се изгради в десет кубически метра. Така се получава, че желаната стойност е 1000 дм 3. Остава да го превърне в м 3. Както в предходния проблема, разделянето се извършва три пъти, само делител ще бъде 10. Тъй като едно m десет дециметра. След разделяне на получения отговор, равен на 1 m 3.: равен обем на 1 м 3.

Третата цел. Дан куб с диагонал дължина от неговите повърхности, равна на √2 мм. Трябва да се изчисли силата на звука.

Осма формула ще ви помогне в това как да намерите отговор на този проблем. Първата стъпка е да се изгради един куб в известно количество. Корен квадратен от 2 в трета степен ще даде стойност 2√2. След умножаване с √2 получите броя 4. Последната стъпка е необходимо да го разделим на 4. Отговор: Обемът на куб 1 mm 3.

Четвъртата цел. Известно е, че диагонала на куба е равно на 3 м. Е необходимо да се изчисли обема си.

Ще просто да намерите отговор на този проблем в съответствие с формулата на номер 9. Стойността, която се дава в състоянието, необходимо е да се изгради един куб. Включете 27. След нейното разпадане на 9 ще отговори е 3. И последното действие тя трябва да бъде умножена по корен квадратен от 3. Задачата за отговор ще 3√3 m3.