Графично разтвор на квадратно уравнение

Графично разтвор на квадратно уравнение

С квадратно уравнение, които вече са се срещали в хода на алгебра в 7-ми клас. Припомнете си, че квадратно уравнение се нарича уравнение на формуляра ос 2 + BX + с = 0, където А, В, С - всички числа (съотношения), характеризиращ се с това. С помощта на нашите познания за някои от функциите и техните графики, ние дори и сега сме в състояние да, без да се чака за системното изучаване на темата "квадратно уравнение" (това ще бъде по-късно, в глава 4), за решаване на някои квадратно уравнение, и по различни начини; Ние считаме, че тези методи по примера на квадратното уравнение.

Пример. За решаване на уравнение х 2 - 2х - 3 = 0.
Решение.
метод аз. Начертава се функция у = х 2 - 2х - 3, като се използва алгоритъма на § 13:

1) имаме = 1, б = -2, x0 = 1, Y0 = F (1) = 1 2 - 2 - 3 = -4. Следователно, на върха на параболата е точка (1; 4) и оста на парабола - правата линия х = 1.

2) поеме х-ос две точки симетричен по отношение на оста на парабола, например х = 1 и х = 3.

3) След точка (-1, 0), (1, -4), (3, 0) провеждане на парабола (виж фигура 68) ..

Корените на уравнение х 2 - 2х - 3 = 0 е абсцисата на параболата точките на пресичане с оста х; означава корените на уравнението са x1 = - 1 х с 2 - 3.

Метод II. Ние трансформиране на уравнението на формата х 2 = 2х + 3. разположен в една графика координатна система функции у - х 2 и Y = 2х + 3 (Фигура 69). Те се пресичат в две точки А (- 1, 1) и В (3, 9). Корените на уравнението са абсцисната на точки А и В, след което Х1 = - 1, X 2 - 3.

III процес. Ние трансформиране на уравнението на формата х с 2 - 3 = 2x. Построява функции на графика координатна система у = х с 2 - 3 и у = 2 (Фигура 70). Те се пресичат в две точки на А (-1 - 2) и В (3, 6). Са корените на абсцисата точки А и В, обаче = x1 - 1, Х2 = 3.

Метод IV. Transform уравнението в х 2 -2x 4-1-4 = 0
и по-нататък
х 2 - 2х + 1 = 4, което е (х - .. IJ = 4.
Ние конструкт в една координатна система, на парабола Y = (х - 1) 2 и у линия = 4 (Фигура 71). Те се пресичат в две точки на А (1, 4) и В (3, 4). Корените на уравнението са абсцисната на точките А и В, следователно, Х1 = -1, Х2 = 3.

метод V. Termwise Разделяне двете страни от х, получаваме

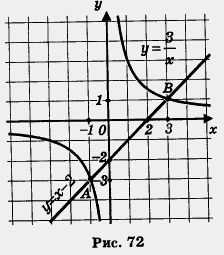
Ние конструкт в една координатна система, хипербола и линията Y права = х - 2 (Фигура 72)..

Те се пресичат в две точки на А (-1, -3) и В (3, 1). Са корените на абсцисата точките А и В, следователно, Х1 = - 1, х2 = 3.

Така че квадратното уравнение х 2 - 2x - 3 = 0, ние решихме да графично пет начина. Нека да анализираме това, което е същността на тези методи.

метод аз. Изобразените функция на неговата точка на пресичане с оста х.

Метод II. Преобразуване на уравнението на форма ос 2 = -BH - за изграждане на парабола Y = брадва 2 и линия у = -BH - да намерят пресечна точка (корени на уравнението са абсцисната на точките на пресичане, разбира се, ако има такива).

III процес. Уравнение се превръща в форма ос 2 + с = - BX строителство парабола у - брадва 2 + С и у = линия -BH (тя преминава през началото); намери точката на пресичане.

Метод IV. Прилагането на метода за разпределение на точен квадрат се превръща в формата на уравнение

и (х + L) 2 + m = О
и по-нататък
и (х + l) = - м

Изграждане парабола у = а (х + I) 2, и у = линия - m, успоредна на оста х; намери точката на пресичане на парабола и една права линия.

метод V. Конвертиране на уравнението на формата

Изграждане хипербола (това - хипербола условие че) и права линия Y = - A - б; намери точката на пресичане.

Имайте предвид, че първите четири режими са приложими за всяка от уравненията на форма ос 2 + BX + с = 0, пет - само тези, в които р. На практика, можете да изберете начина, по който мислите, че най-подходящ за дадено уравнение, или която ви харесва (или не разбира).

Забележка. Въпреки изобилието от методи на графични решения на квадратно уравнение, увереност в това, че който и да е квадратно уравнение можем да решим графично, не. Да предположим, например, е необходимо да се реши уравнението х 2 - х - 3 = 0 (по-специално се вземат уравнението, което е подобно на това, което беше обсъдено в примера). Опита да се реши, например, втория метод: трансформиране на уравнението в х 2 = х 3 + изграждане парабола у = 2 и
линия у = х + 3, те се пресичат в точки А и В (фиг. 73), след това уравнение има две корени. Но какво са тези корени, не можем да кажем на рисунката - точка А и Б не са толкова "добри" позиция, както в примера по-горе. А сега да разгледаме уравнението х 2-95 = 0. 16h- опитаме да го решим, например, на третия метод. Ние трансформиране на уравнението на формата х 2-95 = 16x. Тук е необходимо да се изгради парабола Y = х 2-95, и линията у = 16x. Но ограниченият размер лист от тетрадка не позволяват това да се направи, тъй като парабола у = х 2 трябва да бъде намалена до 95 клетки надолу.

Така графични решения на квадратно уравнение хубаво и приятно, но не дават абсолютна гаранция за решения от всякакъв квадратно уравнение. Ние ще го разгледа, • други.

Математика изтегляне. задача студентски 8 клас материали по математика за 8 клас онлайн

Ако имате корекции или предложения на този урок, моля свържете се с нас.

Ако искате да видите и другите корекции и предложения за уроци, погледнете тук - Образователен форум.