Графичният метод за решаване на уравненията на алгоритъма и примери на графики
основен Nbsp> Nbsp страница-Упътване Nbsp> Nbsp математика Nbsp> nbsp8 клас Nbsp> nbspGrafichesky начин за решаване на уравнения: алгоритъм и графиците примерни
Един от начините за решаване на уравненията е графично начин. Тя се основава на функциите на диаграми и определяне на пресечните им точки. Разглеждане на графичен метод за решаване на квадратното уравнение * х ^ 2 + б * х + С = 0.
Първият начин за решаване на
Ние трансформира уравнение * х ^ 2 + б * х + С = 0 до формата на * х ^ 2 = Ь * Х-С. Парцел графики на две функции у = А * х ^ 2 (парабола) и у = Ь * Х-С (директно). Търсим точката на пресичане. Абсциси на точките на пресичане и ще бъде решение на уравнението.
Ние ще покаже един пример: за решаване на уравнение х ^ 2-2 * х-3 = 0.
Ние я превърне в х ^ 2 = 2 * х + 3. Ние конструкт в една координатна система графики функция у = х ^ 2 и у = 2 * х + 3.

Графиките пресичат в две точки. Тяхната абсциса ще бъде корените на уравнението.
Решението по формулата
За да проверите достоверността на това решение аналитично. Нека да решим квадратно уравнение по формулата:
Така че решения са едни и същи.
Графичен метод за решаване на уравнения, има недостатък, с помощта на не винаги е възможно да се получи точно решение на уравнението. Нека се опитаме да решим уравнението х ^ 2 = 3 + х.
Ние конструкт в една координатна система, на парабола Y = X ^ 2 и линия у = 3 + х.
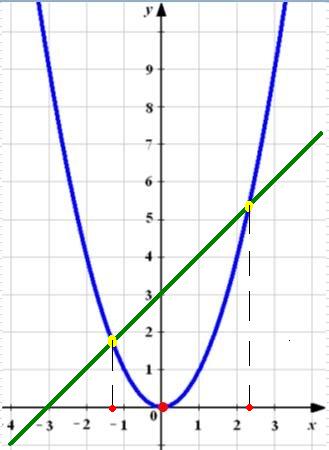
Отново получил подобен модел. Директен парабола и се пресичат в две точки. Но точната стойност на абсцисата на точката не можем да кажем, само приблизителна: x≈-1,3 x≈2,3.
Ако сте доволни от отговорите на такава точност, че е възможно да се използва този метод, но това се случва рядко. Обикновено са необходими точни решения. Ето защо, графичен метод, използван рядко, и най-вече за проверка на съществуващите решения.