Алгебра в 8-ми клас, клас графични решения на квадратно уравнение
Представянето и урока на тема "Графично решение на квадратно уравнение"
Обучаващи пособия и симулатори онлайн магазин "Интеграл" за 8-ми клас
Специалности и корени Функции и графики
Графики на квадратна функция
В последния урок научихме как да се изгради графика на всяка квадратна функция. С помощта на тези функции, можем да решим така наречените квадратно уравнение, които са написани в общ вид, както следва: $ брадва ^ 2 + BX + C = 0 $,
$ A, B, C $ - произволен брой, но долара ≠ 0 $.
Момчета, да сравните уравнение написано по-горе и това: $ у = брадва ^ 2 + BX + C $.
Те са почти идентични. Разликата е, че вместо $ у $ на записахме $ 0 $, т.е. $ Y = 0 $. Как тогава да се реши квадратно уравнение? Първото нещо, което идва на ум, е необходимо да се парцел парабола $ брадва ^ 2 + BX + C $ и да намерят пресечната точка на графиката с линията $ у = 0 $. Има и други начини за решаване. Помислете за тяхното конкретен пример.
Методи за решаване на квадратна функция
Пример.
Решаване на уравнението: $ х ^ 2 + 2 х-8 = 0 $.
Решение.
1. Метод изграждане на графиката на $ Y = х ^ 2 + 2 х-8 $ и да намерят точката на пресичане с линия $ у = 0 $. Коефициентът на най-високата мощност е положителен, тогава бранш парабола да вдига поглед. Намираме координатите на върховете:
$ X _ = - \ Frac = \ Frac = -1 $.
$ Y _ = (- 1) ^ 2 + 2 * (- 1) -8 = 1-2-8 = $ -9.
Точка с координатите $ (- 1; -9) $ се приема като началото на нова координатна система и изграждане на график парабола $ Y = х ^ 2 $.
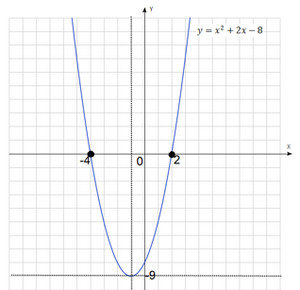
Виждаме две точки на пресичане. с черни точки върху графиката Те са маркирани. Ние решаваме уравнението за х, така че трябва да изберете абсцисната на тези точки. Те са $ -4 $ и $ 2 $.
Така, разтворът на квадратно уравнение $ х ^ 2 + 2х-8 = 0 $ два корени: $ x_1 = -4 и $ $ x_2 = $ 2.
Метод 2: Трансформация на първоначалното уравнение на формата: $ х ^ 2 = 8-2x $.
По този начин може да реши това уравнение от обичайната графичен метод, намирането на абсциси на точките на пресичане на две графики $ Y = х ^ 2 $ и $ у = 8-2x $.

Получените две точки на пресичане, абсцисата на които съвпадат с тези, получени в първите решения на процеса, а именно: $ x_1 = -4 $ и $ x_2 = 2 $.
Метод 3.
Ние трансформира първоначалната уравнението към тази форма: $ х ^ 2-8 = -2x $.
Ние изгради две графики $ у = х ^ 2-8 $ и $ у = -2x $ и намерят точка на пресичане.
График $ у = х ^ 2-8 $ парабола се компенсира от 8 единици надолу.

Получените два пресечните точки, на абсцисата на тези точки са същите, както в предишните два метода, а именно: $ x_1 = -4 $ и $ x_2 = $ 2.
Метод 4.
Изолират пълен квадратен в първоначалното уравнение: $ х ^ 2 + 2х-8 = х ^ 2 + 2х + 1-9 = (х + 1) ^ $ 2-9.
Ние изгради две графики на функции $ Y = (х + 1) ^ 2 $ и $ у = 9 $. Графиката на първата функция е парабола изместен с една единица на ляво. Графиката на втората функция - това е линия, паралелна на оста х и минаваща през ординатата равна на $ 9 $.

Отново има две точки на пресичане на графиките, на абсцисната на тези точки съвпадат с тези, получени при предишните процеси $ x_1 = -4 и $ $ x_2 = 2 $.
Метод 5.
Ние разделят първоначалното уравнение от х: $ \ Frac + \ фракционатор \ Frac = \ Frac $.
$ X + 2- \ Frac = 0 $.
$ X + 2 = \ Frac $.
Ние решаване на това уравнение графично изграждане две графики $ у = х + 2 $ и $ у = \ Frac $.
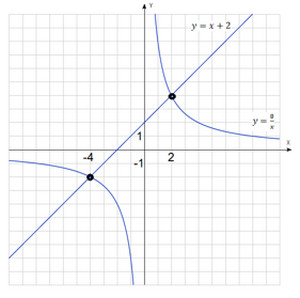
Отново получи две пресечните точки, на абсцисата на точките съвпадат с тези, получени по-горе $ x_1 = -4 $ и $ x_2 = $ 2.
Алгоритъм графичен разтвор на квадратна функция
Момчета, ние сме считани за пет методи на графични решения на квадратно уравнение. Във всеки от тези начини корените на уравнения се оказаха едни и същи, което означава, че се получава правилното решение.
Основните методи на графични разтвори на квадратно уравнение $ брадва ^ 2 + BX + C = 0 $ $ а, Ь, с $ - произволен брой, но долара ≠ 0 $:
1. изграждане на графика на $ у = брадва ^ 2 + BX + в $, намери точка на пресичане с оста х, която ще бъде разтвор от уравнението.
2. Изграждане две графики $ у = брадва ^ 2 $ и $ у = -bx-с $, намери абсцисата на пресечните точки на тези графики.
3. Изграждане две графики $ у = брадва ^ 2 + C $ и $ у = -bx $, намери абсцисата на пресечните точки на тези графики. Графиката на първата функция е парабола, или изместен надолу или нагоре, в зависимост от броя на знак с. Вторият графиката - линията, преминаваща през началото.
4. Избор на точен квадрат, който се въвеждат оригиналната уравнението на формата: $ а (х + л) ^ 2 + m = 0 $.
За изграждането на два от графиката на $ у = а (х + л) ^ 2 $ и $ у = -m $, намерят точка на пресичане. Графиката на първата функция е парабола изместен или наляво или надясно, в зависимост от знака на числото $ л $. Графиката на втората функция е права линия, успоредна на оста на абсцисата и ординатната ос пресичащи се в една точка, равен на $ -м $.
5. Разделете първоначалното уравнение от х: $ брадва + B + \ Frac = 0 $.
Конвертиране в следния вид: $ \ Фрак = -ax-б $.
Отново се изгради две графики и да намерят пресечни точки. Първата графика - хипербола, втората графика - е права. За съжаление, графичен метод за решаване на квадратно уравнение не винаги е добър начин за решаване. пресечните точки на различните класации не винаги са цели числа, или може да се наложи в абсциса (ординатата) много големи числа, които не се основават на стандартен лист хартия.
По-ясно демонстрира всички тези техники пример.
Пример.
Решаване на уравнението: $ х ^ 2 + 3x-12 = 0 $,
Решение.
Ние построи графиката на параболата и да намерят координатите на върховете: $ х _ = - \ Фрак = \ Фрак = -1,5 $.
$ Y _ = (- 1,5) ^ 2 + 2 * (- 1,5) -8 = 2,25-3-8 = -8,75 $.
При конструирането на парабола, след като възникнат проблеми, например, правилно, за да отбележат началото на параболата. С цел да се отбележат точно съгласува върховете трябва да изберете една клетка, равна на 0,25 единици мащаб. На този мащаб, за да се понижат с 35 единици надолу, което е неудобно. И все пак, ние конструираме нашия график.

Вторият проблем пред който сме изправени, е, че нашата функция графика пресича оста х в точката с координати, които определят точно невъзможно. Може би приблизителна решение. но по математика - това е точна наука.
По този начин, графичен метод не е най-удобно. Следователно, за да се реши квадратно уравнение изисква универсален метод, който ще разгледаме в следващия урок.
Задачи за независим решение
1. решаване на уравнението графично (всички пет начина): $ х ^ 2 + 4x-12 = 0 $.
2. решаване на уравнение графично начин: $ -х ^ 2 + 6x + $ 16 = 0.