Аксиома геометрия и ефект от тях

Геометрия - науката за пространствени форми и количествените характеристики на реални обекти.

Строителство геометрия като наука се състои от избора на основни геометрични понятия, основните свойства на състава на тези геометрични понятия чрез твърдения, които са истински, без доказателство, строителни и други концепции. Тази конструкция се нарича аксиоматична.

Аксиома - това твърдение се приема за истина, без доказателства.

Човек може да помисли за геометрията на самолета и в пространството. Геометрията на равнината се нарича планиметрия в пространството - стереометрия.

Неоткриваем или основни понятия са планиметрия точка. с права, и в твърда геометрия - точка, линия и равнина.

основни геометрия аксиоми на

Аксиома геометрия могат да бъдат разделени в пет групи.

1. аксиоми аксесоари

1.1 Каквато и да е прав, че има точки, които принадлежат към нея и не принадлежат към нея.

1.2 Чрез всеки две точки, можете да нарисувате права един и само един.

1.3 Каквато и да е равнина, има точки, които принадлежат към тази плоскост, както и точки, които не принадлежат към нея.

2. аксиоми място

2.1 От трите точки на линията, един и само един се намира между другите две.

2.2 Директен разделя равнината на две половини равнини.

2.3 Ако две различни линии имат обща точка, чрез тях можете да прекарате на самолета и, освен това, само един.

2.4 Ако две различни равнини имат обща точка, а след това те се пресичат в една права линия, минаваща през тази точка.

3. Измерване аксиоми

3.1 Всеки сегмент има определена дължина по-голяма от нула. Дължина на маршрута, равна на сумата от дължините на частите, в които тя се разпада му всеки момент.

Всеки ъгъл 3.2 градуса има известна степен по-голяма от нула. Разширен ъгъл е. Степен мярка на ъгъл, равен на степента на сума ъгли мерки, за които е разбита от всеки лъч преминаване между страните.

4. аксиоми рафтове.

4.1 Във всеки половината от първоначалната си точка на сегмента може да се забави с предварително определена дължина и само един.

4.2 От всяка половина половината равнина в предварително определен ъгъл може да се забави с предварително определена мярка степен в една и само една.

4.3 Каквато и да е триъгълник, има триъгълник е равен на него, в предварително определено място в сравнение с този период на линия.

5. Аксиома на паралелизъм.

5.1 Чрез точка не по дадена линия може да побере не повече от една линия, успоредна на тази.

Примери за решаване на проблеми

Две равнини и се пресичат в една права линия. Директен и кръст. Къде е пресечната точка на линиите и?

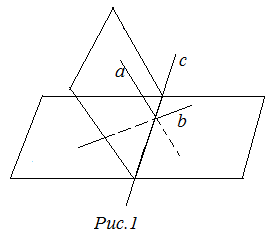
Ако две равнини се пресичат в една права линия, а след това всички точки, които линия принадлежат както на първия и втория равнини. Тъй като прави и лъжата в различни равнини и по този начин се пресичат, а след това им пресичане точка принадлежи на двете равнини и, очевидно, се намира на линията.

пресечната точка на правите линии и се намира на линията.

Определи максималния възможен брой самолети може да се направи чрез лъч данни 3 с обща начална точка (няма две греди лежат на една права линия)?

Според аксиома 2.3 чрез всеки две линии с обща точка може да се осъществи една равнина. Ето защо, ако три греди не се намират в една и съща равнина, те могат да бъдат разделени в три различни двойки от лъчи. Тогава най-големият брой на самолети, които могат да носят, е три.

3 максимална лъч данни можете да прекарате три равнини.